728x90
더보기
추천 시스템 관련 논문 읽어 보다가 개념 정리가 잘 안되어 있다고 판단되서 글 작성해봅니당 :) !!
1. MF (Matrix Factorization)
- 선형대수학의 SVD(Singular Value Decomposition)를 응용한 방법론
- 하나의 행렬을 여러 행렬로 분할한다는 관점

- 기존의 분할된 행렬에서 핵심 정보만을 사용한다는 효율적인 개념
- Full SVD에서 특이값이 높은 상위 k개 를 사용하여 Truncated SVD 구현
- Full SVD의 도출값인 A는 Truncated SVD의 도출값과 유사할 것이라는 관점

- MF는 Truncated SVD의 왼쪽 두 행렬을 user latent matrix로 사용
- MF는 Truncated SVD의 오른쪽 한 행렬을 item latent matrix로 사용
- 이때 k는 잠재 요인의 개수를 의미
- User-Item Rating 행렬의 예측값 R_hat 도출


- 잠재요인 k 설정
- user latent matrix P 행렬 생성
- item latent matrix Q 행렬 생성
- P 행렬과 Q 행렬을 기반으로 예측 평점 R_hat 도출
2. MF Algorithm
- 잠재 요인 개수인 k 설정
- k에 따라 user latent matrix P 행렬과 item latent matrix Q 행렬 생성 후, 초기화 진행
- user latent matrix P 와 item latent matrix Q를 이용하여 예측 평점 R_hat 도출
- 실제 평점 R과 예측 평점 R_hat의 오차 도출
- 오차를 줄이기 위해 user latent matrix P와 item latent matrix Q의 값을 업데이트
- 오차가 일정 Threshold 이하가 되거나 미리 정해진 Iteration에 도달할 때 까지, 세번째 과정으로 돌아가 반복
3. Objective Function

- 오차를 최소화하며 Overfitting과 Underfitting을 방지하기 위해 L2 정규화 사용
4. Optimazation (SGD)

- 목적함수 L을 최소화하는 최적화 기법으로 SGD (Stochastic Gradient Descent) 활용
- 위의 식은 p에 대하여 편미분 진행
- 아래 식은 q에 대하여 편미분 진행
더보기



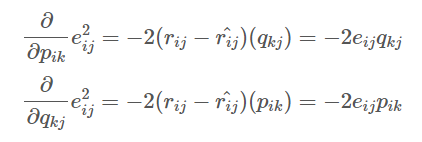
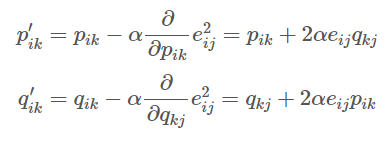
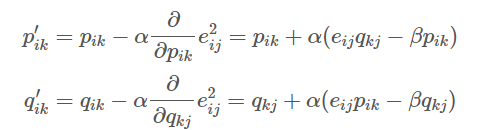

- P 행렬과 Q행렬을 기반으로 예측 평점 도출

- 실제 평점 R과 예측 평점 R_hat의 차를 통해 예측 오차 도출

- 오차 제곱을 최소화해야 하므로, 오차의 제곱식 도출
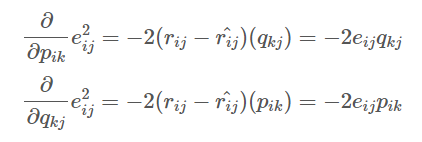
- 오차 제곱식에서 편미분을 진행
- 위의 식은 p에 대해 편미분 진행
- 아래 식은 q에 대해 편미분 진행
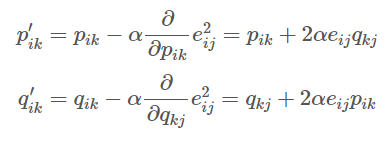
- 위에서 도출된 결과를 기반으로 업데이트 될 p 와 q 값
- a는 학습률
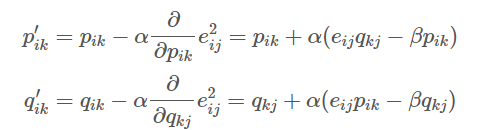
- 정규화식을 고려하여 도출된 업데이트 될 p 와 q 값
- a는 학습률
5. Adding Biases
- 사용자의 취향 등에 따라 편향된 평점이 존재
- 사용자의 취향과 별개로 아이템이 유명한 명장 등의 이유로 편향된 평점이 존재
- 따라서 사용자가 가진 편향과 아이템이 가진 편향을 고려해야 함
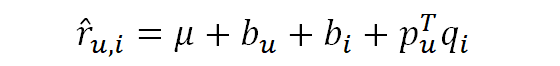
- 사용자가 가진 편향(b_u)과 아이템이 가진 편향(b_i)을 기반으로 예측 평점 R_hat 재설정
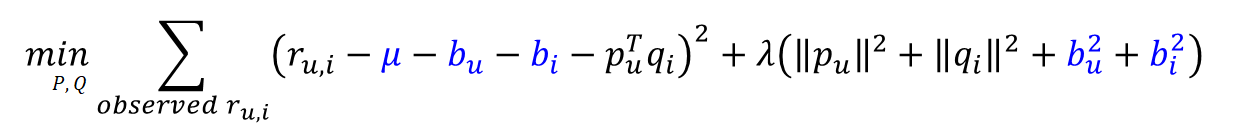
- 사용자가 가진 편향(b_u)과 아이템이 가진 편향(b_i)을 기반으로 목적 함수 재설정
6. Example Code
class MF():
def __init__(self, ratings, K, alpha, beta, iteration, verbose=True):
self.R = np.array(ratings) # 원행렬
self.num_users, self.num_items = np.shape(self.R) # 유저, 아이템 수
self.K = K # 잠재요인 수
self.alpha = alpha # 학습률
self.beta = beta # 정규화 계수
self.iteration = iteration # 반복횟수
self.verbose = verbose # 중간과정 표시
def RMSE(self):
xs, ys = self.R.nonzero()
self.predictions = []
self.errors = []
for x, y in zip(xs, ys):
prediction = self.get_prediction(x, y)
self.predictions.append(prediction)
self.errors.append(self.R[x, y] - prediction)
# 계산을 위해 numpy array로 변경
self.predictions = np.array(self.predictions)
self.errors = np.array(self.errors)
return np.sqrt(np.mean(self.errors**2))
def train(self):
# 초기값 설정
self.P = np.random.normal(scale=1./self.K, size=(self.num_users, self.K))
self.Q = np.random.normal(scale=1./self.K, size=(self.num_items, self.K))
# bias 초기값 설정
self.b_u = np.zeros(self.num_users)
self.b_d = np.zeros(self.num_items)
self.b = np.mean(self.R[self.R.nonzero()])
# 값이 존재하는 data 불러오기
rows, columns = self.R.nonzero()
self.samples = [(i, j, self.R[i,j]) for i, j in zip(rows, columns)]
# SGD 진행
training_process = []
for i in range(self.iteration):
np.random.shuffle(self.samples)
self.sgd()
rmse = self.RMSE()
training_process.append((i+1, rmse))
if self.verbose:
if (i+1) % 10 == 0:
print("Iteration: %d : Train RMSE = %.4f " % (i+1, rmse))
return training_process
def get_prediction(self, i, j):
prediction = self.b + self.b_u[i] + self.b_d[j] + self.P[i,:].dot(self.Q[j,:].T)
return prediction
def sgd(self):
for i, j, r in self.samples:
prediction = self.get_prediction(i, j)
e = (r - prediction)
self.b_u[i] += self.alpha * (e - self.beta * self.b_u[i])
self.b_d[j] += self.alpha * (e - self.beta * self.b_d[j])
self.P[i, :] += self.alpha * (e * self.Q[j, :] - self.beta * self.P[i,:])
self.Q[j, :] += self.alpha * (e * self.P[i, :] - self.beta * self.Q[j,:])
References
- https://datajobs.com/data-science-repo/Recommender-Systems-[Netflix].pdf
- https://sungkee-book.tistory.com/12
- https://bladejun.tistory.com/57
'AI > Machine Learning' 카테고리의 다른 글
| FM (Factorization Machine) (0) | 2023.03.05 |
|---|---|
| [Practical Time Series Analysis (실전 시계열 분석)] Chapter 06 시계열의 통계 모델 (0) | 2022.03.23 |
| [Practical Time Series Analysis (실전 시계열 분석)] Chapter 05 시간 데이터 저장 (0) | 2022.03.23 |
| [Practical Time Series Analysis (실전 시계열 분석)] Chapter 04 시계열 데이터의 시뮬레이션 (0) | 2022.03.22 |
| [Practical Time Series Analysis (실전 시계열 분석)] Chapter 03 시계열의 탐색적 자료 분석 (0) | 2022.03.20 |



