목차
- 시간 복잡도란?
- Big-O 란?
- Big-O 의 종류
- Big-Ω 란?
- Big-Ω 의 종류
- Big-O가 낮은 알고리즘이 좋을까? Big-Ω가 낮은 알고리즘이 좋을까?
시간 복잡도란?
시간 복잡도란 입력값과 문제를 해결하는 데 걸리는 시간을 함수 관계로 나타낸 것 이다.
즉 실행시간을 기준으로, 알고리즘이 얼마나 효율적인지를 판단할 수 있는 척도이다.
시간 복잡도는 최악의 경우, 최선의 경우, 평균의 경우를 계산해서 나타낸다.
이때 최악의 경우는 Big-O(빅-오), 최선의 경우는 Big-Ω(빅-오메가), 평균의 경우는 Big-θ(빅-세타)로 나타 낸다.
이번 글은 Big-O(빅-오)와 Big-Ω(빅-오메가)에 대한 내용만 다룰 것 이다.
Big-O 란?
Big-O(빅-오) 란, 위에서 언급했듯이 최악의 경우를 나타낸 것이다.
즉 Big-O는 알고리즘을 실행시켰을 때, 최대로 걸릴 수 있는 시간(상한 시간)을 말한다.
그러므로 Big-O가 높을수록, 최악의 경우에 알고리즘이 매우 오래 걸릴 수 있다.
Big-O 의 종류
| 종류 | 의미 |
| O(2ⁿ) | n개를 입력했을 때, 최악의 경우 2ⁿ번 실행된다. |
| O(n³) | n개를 입력했을 때, 최악의 경우 n³번 실행된다. |
| O(n²) | n개를 입력했을 때, 최악의 경우 n²번 실행된다. |
| O(n log n) | n개를 입력했을 때, 최악의 경우 n log n번 실행된다. |
| O(n) | n개를 입력했을 때, 최악의 경우 n번 실행된다. |
| O(log n) | n개를 입력했을 때, 최악의 경우 log n번 실행된다. |
| O(1) | n개를 입력했을 때, 최악의 경우 1번 실행된다. |
위의 Big-O 의 종류를 정리한 표를 보면, 최악의 경우에 2ⁿ번 실행되는 O(2ⁿ)이 가장 비효율적이라는 것을 알 수 있다.
왜냐하면 충분히 적은 시간으로 해결할 수 있는 문제를, 굳이 시간을 더 들여서 해결하는 것은 비효율적이기 때문이다.
다른 의미로, 최악의 경우에 1번 실행되는 O(1)이 가장 효율적이라는 것을 알 수 있다.
왜냐하면 최악의 경우에 단 1번의 실행으로 문제를 해결할 수 있기 때문이다.
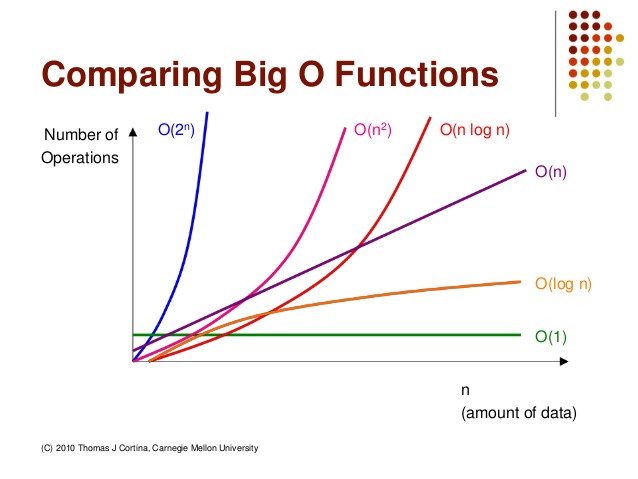
위의 Big-O를 그래프로 나타내면 위의 그림과 같다.
그림에서도 볼 수 있듯이, O(2ⁿ)이 같은 입력 개수를 넣더라도 실행시간이 가장 오래 걸린다는 것을 알 수 있다.
그리고 O(1)은 무한한 입력 개수를 넣더라도 실행시간은 1로 일정한 것을 확인할 수 있다.
그러므로 시간 복잡도의 효율성은 O(2ⁿ)<O(n³)<O(n²)<O(n log n)<O(n)<O(log n)<O(1) 인 것이다.
Big-Ω 란?
Big-Ω(빅-오메가) 란, 위에서 언급했듯이 최선의 경우를 나타낸 것이다.
즉 Big-Ω는 알고리즘을 실행시켰을 때, 최소로 걸릴 수 있는 시간(하한 시간)을 말한다.
그러므로 Big-Ω가 낮을수록, 최선의 경우에 알고리즘이 매우 빠르게 진행될 수 있다.
Big-Ω 의 종류
| 종류 | 의미 |
| Ω(2ⁿ) | n개를 입력했을 때, 최선의 경우 2ⁿ번 실행된다. |
| Ω(n³) | n개를 입력했을 때, 최선의 경우 n³번 실행된다. |
| Ω(n²) | n개를 입력했을 때, 최선의 경우 n²번 실행된다. |
| Ω(n log n) | n개를 입력했을 때, 최선의 경우 n log n번 실행된다. |
| Ω(n) | n개를 입력했을 때, 최선의 경우 n번 실행된다. |
| Ω(log n) | n개를 입력했을 때, 최선의 경우 log n번 실행된다. |
| Ω(1) | n개를 입력했을 때, 최선의 경우 1번 실행된다. |
위의 Big-Ω 의 종류를 정리한 표를 보면, 최선의 경우에 2ⁿ번 실행되는 O(2ⁿ)이 가장 비효율적이라는 것을 알 수 있다.
왜냐하면 충분히 적은 시간으로 해결할 수 있는 문제를, 굳이 시간을 더 들여서 해결하는 것은 비효율적이기 때문이다.
다른 의미로, 최선의 경우에 1번 실행되는 Ω(1)이 가장 효율적이라는 것을 알 수 있다.
왜냐하면 최선의 경우에 단 1번의 실행으로 문제를 해결할 수 있기 때문이다.
Big-O가 낮은 알고리즘이 좋을까? Big-Ω가 낮은 알고리즘이 좋을까?
가장 이상적인 것은 Big-O와 Big-Ω 가 동시에 낮은 알고리즘이다.
왜냐하면 최악의 상황과 최선의 상황에서 실행시간이 낮을수록 효율적이기 때문이다.
하지만 실제로 둘 다 동시에 낮은 알고리즘이 존재하지 않는 것으로 알고 있다.
대부분의 알고리즘은 Big-O와 Big-Ω이 반비례 관계에 있기 때문이다.
그래서 굳이 Big-O와 Big-Ω 중 어느 것이 낮은 알고리즘을 택할 것인지 골라야한다면,
Big-O가 낮은 알고리즘을 택할 것이다.
왜냐하면 코드를 작성하다 보면, 최선의 상황을 마주하기 보단 최악의 상황을 마주하는 경우가 많기 때문이다.
그래서 최선의 경우 보단 최악의 경우를 대비하여, Big-O 실행시간을 줄이는 것이 가장 현실적인 선택이라고 생각한다.
위 글은 edwith 사이트의 <cs50> 강의 시청과
부스트 코딩 뉴비 챌린지 2020 활동 팀원들과 토론을 통해 공부한 내용을 작성한 것 입니다.
내용상 오류가 있다면 댓글로 적어주세요. 🖐
2020/07/23 - [Life/2020] - [대외활동] 부스트 코딩 뉴비 챌린지 2020
[대외활동] 부스트 코딩 뉴비 챌린지 2020
기간 2020 / 07 / 10 ~ 2020 / 08 / 28 동기 저번에 빅데이터 전문가 자격증을 공부하고 나서 컴퓨터 기초 지식을 공부할 필요성을 느꼈다. 그래서 공부할 방법을 알아보다가 부스트 코딩 뉴비 챌린지 202
all-young.tistory.com
'CS > Algorithm' 카테고리의 다른 글
| 정렬 알고리즘 (2) (삽입, 퀵 정렬) (0) | 2020.09.04 |
|---|---|
| 정렬 알고리즘 (1) (버블, 선택, 병합(합병) 정렬) (0) | 2020.08.30 |
| 탐색 알고리즘 (검색 알고리즘: 선형검색과 이진검색) (0) | 2020.08.25 |


